Önermeler Mantığı

Formel sistemler şu elemanlardan meydana gelir:

Tanımlanmamış terimler
Tanımlar
Türetme kuralları
Aksiyomlardır
Teoremler

Formel mantığın tanımlanmamış terimleri olarak, basit önerme (P) ve mantıksal bağlar (değil, ve, veya, eğer-ise, eğer ve ancak-ise) gösterilebilir.

Tanımlanan terimlere örnek olarak bileşik önerme kavramını gösterilebilir. Aslında yukarıda verilen mantıksal bağlar bir tek mantıksal bağ yardımıyla tanımlanabilir.

Önerme

Aşağıdaki cümleler önermelere örnektir:

Bugün hava güneşlidir.
3 asal sayıdır.
Duygu 21 yaşındadır.
3 asal sayı değildir.
Duygu 21 yaşında değildir.
Bir gün 24 saattir.

Mantıksal bağlar kullanarak basit önermelerden başka önermeler kurulabilir, ki bunlara “bileşik önermeler” denir.Önerme matematikte kesin bir hüküm bildiren ifadelere denir.

Olumsuzu

Bir önerme “değil” eki ile karşıt ifadeye çevrilebilir; buna değilleme denir.

Bir hafta 7 gün'dür. Bir hafta yedigün degildir.

Birleşim

İki veya daha fazla önermeden “ve” mantıksal bağını kullanarak bileşik önermeler kurulabilir. Örnek olarak: “Bu gün hava açık ve sıcak” cümlesini verilebilir. Doğal dilde bazen “fakat” bağlacını da kullanıyoruz.

Örnek: “bugün gemiler 9'da ve 10.da sefer yapacak.” değili A' olarak gösterilir

Ayrılım

İki veya daha fazla basit önermeden “veya” (ya da) mantıksal bağını kullanarak bilesik önermeler kurulabilir.

Örnek: “Bugün Arçelik veya Teletaş'tan ziyaretçiler gelecek.”

Şartlı cümle

Aynı şekilde, iki veya daha fazla sayıda önermeden (eğer-ise) bağını kullanarak şartlı önermeler kurulabilir.

Örnek: “Eğer yağmur yağıyor ise, hava bulutludur.”

Bazen “eğer-ise” bağı yerine doğal dilde “gerektirir” bağını da kullanabiliyoruz.

Örnek: “Yağmurun yağıyor olması havanın bulutlu olmasını gerektirir.” Ancak ve Ancak BJKKK

Ancak ve Ancak

Yine, “eğer ve ancak-ise” bağını kullanarak birden fazla önermeden çift şartlı önermeler kurulabilir. Bu tür önermeler doğal dilde daha az kullanılmasına rağmen, fizik ve matematikte sık sık kullanılmaktadır.

Örnek: “Eğer ve ancak çalışanlar ücretlerde aşırı artış talep ederlerse enflasyon düşmez.”

Aynı cümle şu şekilde de ifade edilebilir: “Eğer, çalışanlar ücretlerde aşırı artış talep ederlerse enflasyon düşmez, ve eğer enflasyon düşmezse çalışanlar ücretlerde aşırı artış talep ederler.”

Cebirde olduğu gibi, sembolik veya matematiksel mantıkta da, önermeler yerine önermesel değişkenler kullanılır (P, Q, R, S, T harfleri gibi).

Mantıksal bağlar

Mantıksal bağlar aşağıdaki sembollerle gösterilir:

$neg$ : değil
$land$ : ve
$lor$ : veya
$to$ : eğer-ise
$leftrightarrow$ : eğer ancak-ise

Böylece şu ifadeler, önermesel formüller olacaktır:

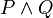$neg P$ , $P land Q$ , $P lor Q$ , $P to Q$ , $P leftrightarrow Q$

Örnek: "Eğer sendika veya fabrika yöneticileri inada devam ederlerse, grev ancak hükümet bir kararname çıkarır ve fabrikaya polis göndermezse önlenir."

P: Sendika inada devam eder
Q: Fabrika yöneticileri inada devam eder
R: Grev önlenir
S: Hükümet kararname çıkartır
T: Hükümet fabrikaya polis göndermez

$(P lor Q) to (R leftrightarrow S land T)$

Doğruluk cetvelleri

Mantıkta önermeler doğru ya da yanlış olabilir, fakat hem doğru hem yanlış olamaz. Bir önermeye yüklenen bu “doğru” ve “yanlış” yüklemlerine onun “doğruluk değeri” denir.

Buna göre, şimdi şu önermesel formüllerin doğruluk değerlerini irdeleyelim:

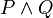$neg P$ , $P land Q$ , $P lor Q$ , $P to Q$ , $P leftrightarrow Q$

“Değil” sözcüğünün anlamından hareketle, eğer bir P önermesi doğru ise onun değillemesi, yani $neg P$ yanlıştır, ve bunun tersi. Mesela, P önermesi “Ay dünyanın uydusudur” cümlesi yerine geçiyorsa, bunun değillemesi olan $neg P$ yanlıştır.

Gene, kural olarak iki veya daha fazla önermenin birleşimi, ancak birleşen bütün önermelerin doğru olması halinde doğrudur. Mesela, “3 asal sayıdır ve 2+2=5'tir” yanlış bir bileşik önermedir.

Yine kural olarak, ayrık önermelerin doğru olabilmesi için bileşenlerden birinin doğru olması yeterlidir. Ayrık önermeler ancak bunları meydana getiren bileşenlerin hepsinin birden yanlış oldugu halde yanlış sayılır.

Bileşik önermeler için doğruluk tabloları şu şekilde verilebilir:

$P$	$Q$	$neg P$	$P land Q$	$P lor Q$	$P to Q$	$P leftrightarrow Q$
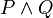D	D	Y	D	D	D	D
D	Y	Y	Y	D	Y	Y
Y	D	D	Y	D	D	Y
Y	Y	D	Y	Y	D	D

D: doğru, Y: yanlış

Eşdeğerlikler

$neg neg P = P$
$neg P lor Q = P to Q$
$neg (P lor Q) = neg P land neg Q$
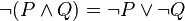
$neg (P land Q) = neg P lor neg Q$

Karşıtlıklar

$neg P times P$
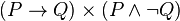
$(P to Q) times (P land neg Q)$
$(P lor Q) times (neg P land neg Q)$
$(P land Q) times (neg P lor neg Q)$

Totoloji: Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki bütün değerler “doğru” çıkıyorsa, bu önermesel formüle “totoloji” denir.

Çelişki: Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki bütün değerler “yanlış” çıkıyorsa bu önermesel formüle “çelişki” denir.

Bazen doğruluk: Bir önermesel formülün (veya bileşik önermenin) doğruluk cetvelindeki son değerlendirme sütunundaki değerlerden bazıları “doğru” bazıları “yanlış” çıkıyorsa bu önermesel formüle “bazen doğru” denir.

Tutarlılık: Bir bileşik önermeye “ve” ekiyle başka bir önerme eklendiği zaman bir çelişki ortaya çıkmıyorsa, eklenen önerme öncekiyle tutarlıdır denir.

Geçerlilik: Bir A₁, A₂, ..., A_n önerme dizisindeki bütün A’lar doğru olduğu zaman bir B hükmü de doğru oluyorsa B’ye A₁, A₂, ..., A_n önermelerinin geçerli sonucudur denir. Geçerlilik şu şekilde gösterilir:

A₁, A₂, ..., A_n |= B.

Mantıksal İçerik: Bir bileşik önermeyi yanlış yapan şartların sayısının bütün şartların sayısına oranı ne kadar büyükse, o önermenin mantıksal içeriği o kadar fazladır. Çelişkinin mantıksal içeriğinden bahsedilemez (çünkü yoktur.).(-->bu durumda çelişki için mantıksal içerik 1/1 olması beklenir. buna göre ilk cümle ile bahsedilen tanım tersi olarak düşünülmesi gerekmektedir =>düzeltmedir, şayet hata yok ise siliniz?)

Yüklemler Mantığı

Önermeler mantığının türetim kuralları matematik için yeterli olmadığı gibi gündelik dil için de yeterli değildir. Mesela, klasik mantıkta "Her asal sayı bir doğal sayıdır" ve "3 asal sayıdır" öncüllerinden, "3 doğal sayıdır" sonucunu çıkarabiliyoruz. Fakat bu akıl yürütmenin doğruluğu, önermeler mantığının kuralları çerçevesi içinde kanıtlanamaz. Bunun nedeni de şudur: Önermeler mantığı bileşik önermeler içindeki basit önermeler arasındaki mantıksal bağlara ve basit önermelerin doğruluk değerlerine göre bileşik önermelerin doğruluklarını inceler. Diğer bir deyişle, önermeler mantığı bir önermeyi birçok maksat için yeterli ayrıntıda analiz etmez.

İşte, terimler, yüklemler ve niceleyiciler diye isimlendireceğimiz mantıksal kavramlar yardımıyla gündelik dili ve matematiğin dilini büyük ölçüde sembolize edebiliriz.

Yüklemler mantığında da aynı matematikte olduğu gibi, sabitler ve değişkenler kullanılır. Biraz önce bahsedilen "terimleri" iki sınıfa ayırabiliriz: Bireysel değişkenler, bireysel sabitler. Bireysel sabitlere örnek olarak birey olduğunu bildiğimiz varlıkları sayabiliriz: “Gökhan”, “Tekir”, “gül” gibi. Bunlar yerine de “insan”, “hayvan”, “bitki” kavramlarının çerçeveleri içinde olmak üzere x, y, z, değişken sembollerini kullanabiliyoruz.

Matematikte değişkenler genellikle sayılar veya fonksiyonlar olabilir. Yüklemler mantığında ise bireysel terimler değişken olabildiği gibi, yüklemler de sabit veya değişken olabilir. Yüklemsel sabitlere örnek olarak önermeler içinde yer alan yüklemleri gösterebiliriz: “sayı”, “meyve”, “uydu”, “sert” gibi. Buna göre,

7 bir asal sayıdır.
Elma bir tür meyvedir.
Miranda, Neptün'ün uydusudur.
Demir sert bir metaldir.

...cümleleri içinde "7", "elma", "Miranda", "Neptün" ve "demir" bireysel sabitler, “asal sayı, “meyve”, “uydu” ve “sert metal” de yüklemsel sabitlerdir.

Yüklemsel ifadelerde yüklemler yukarıdaki örneklerde görüldüğü gibi bir veya iki terimli (veya argümanlı) olabildiği gibi, daha fazla sayıda argüman da içerebilirler. Mesela: “Beril, Akın ve Şebnem'nin önünde oturuyor” dediğimiz zaman, burada “önünde oturuyor” ifadesini yüklem olarak; Beril, Akın ve Şebnem isimlerini de bireysel sabitler olarak almış oluyoruz.

Yüklemsel ifadeler yüklemin aldığı terim sayısına göre şu genel biçimlerde gösterilebilirler:

P(a), Q(b,c), R(d,e,f), ...

Bu ifadelerde, hemen görülebileceği gibi, bireysel sabitler yerine x, y, z gibi değişkenler koyarsak,

P(x), Q(b,y), R(z,e,f)

...gibi değişken terimli yüklemsel ifadeler elde ederiz.

Eşdeğerlik ve karşıtlık

A(x) yüklemsel bir formül olsun. Şu ifadeleri gözönüne alalım:

a) $forall x A(x)$
b) $exists x A(x)$
c) $forall x (neg A(x))$
d) $exists x (neg A(x))$

Bunları doğal dile çevirirsek:

a) Herşey A yüklemine (özelliğine) sahiptir.
b) Bazı şeyler A yüklemine (özelliğine) sahiptir.
c) Hiçbir şey A yüklemine (özelliğine) sahip değildir.
d) Bazı şeyler A yüklemine (özelliğine) sahip değildir.

Burada görüldüğü gibi, d, a'nın karşıtı (değillemesi), c de b'nin karşıtıdır. Şu halde, $exists x A(x)$ yerine $neg forall x neg A(x)$ kullanabiliriz, çünkü bunlar mantıksal olarak özdeştir, aynı şekilde $forall x A(x)$ yerine $neg exists x neg A(x)$ ifadesini kullanabiliriz.

Yüklemsel ifadelerde değilleme ve niceleyicilerin yeri, anlam bakımından önemlidir. Örneğin:

$neg forall x asal(x)$ , “her sayı asal değildir” anlamına gelirken,
$forall x neg asal(x)$ ise “hiçbir sayı asal değildir” anlamına gelir.

Eşdeğerlikler

$forall x P(x) = neg [exists x neg P(x)]$
$exists x P(x) = neg [forall x neg P(x)]$
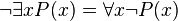
$neg exists x P(x) = forall x neg P(x)$
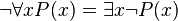
$neg forall x P(x) = exists x neg P(x)$

Karşıtlıklar

$forall x P(x) times exists x neg P(x)$
$exists x P(x) times forall x neg P(x)$
$neg exists x P(x) times exists x P(x)$
$neg forall x P(x) times forall x P(x)$

Çözülüm Teorem İspatlama

Çözülüm teorem ispatlama, mantık teoremlerinin ispatlanması için A. Robinson tarafından geliştirilmiş bir tekniktir. Bu tekniğin esası şudur:

Eğer “ve” bağı ile bağlı P₁, ..., P_n önermelerinden bir Q önermesi dedüktif olarak çıkarılabiliyorsa, o zaman Q'nun değillemesini bu önermelere “ve” bağı ile kattığımız zaman bir çelişki elde ederiz. Sembollerle gösterecek olursak:

$P_1 land, ..., land P_n to Q$

...çıkarımı geçerli ise,

$P_1 land, ..., land P_n land neg Q$

...bir çelişkidir.

Bu yöntemin kullanılabilmesi için, P₁, ..., P_n önermelerinin, eşdeğerlik dönüşümleri kullanılarak “birleşimli normal biçim” denilen bir biçime getirilmesi gerekir. Bu biçim sadece “değil”, “ve” ve “veya” mantıksal bağlarını içerir.

Örnek 1:

P -> Q             ~P V Q          ~P V Q
                     P                   P               P
                     ------             ------          ~Q
                     Q                   Q              ------

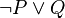Bu örnekte $P to Q$ şartlı önermesi yerine, eşdeğeri $neg P lor Q$ konulmuştur ki bu, $P to Q$ önermesinin normal biçimidir.

Örnek 2:

A -> B             ~A V B           ~A V B
                    B -> C             ~B V C           ~B V C
                    A                   A                A
                   --------           ---------         ~C
                    C                   C              ---------

Çözülüm teorem ispatlama yöntemi, yüklemler mantığının teorem ispatlama problemlerinde de uygulanmaktadır. Yüklemler mantığında teorem ispatı sırasında bireysel sabitlerin değişkenlerin yerine konulmasına “birleştirme” denilir.

Örnek 3:

P(x,y) -> Q(x)           ~P(x,y) V Q(x)          ~P(a,y) V Q(a)
                    P(a,y)                    P(a,y)                  P(a,y)
                    --------------           ---------------         ~Q(a)
                    Q(a)                      Q(a)                   ---------------

Bulanık Mantık

Bulanık mantık 1960’ların ortalarında Lotfi Zadeh tarafından iki değerli mantık ve olasılık teorisine alternatif olarak geliştirilmiştir. Bulanık mantıkçılara göre iki değerli mantık ve kümeler teorisi daha genel çok değerli bir teorinin özel halidir. Zadeh (1965) bulanık kümeleri ve bulanık mantığı şu şekilde tanımlamaktadır: "Bulanık sistemlerde temel düşünce bulanık mantıkta doğruluk değerleri (veya bulanık kümelerde üyelik değerleri) 0 ile 1 arasında değişen değerlerdir ki burada 0 mutlak yanlış, 1 de mutlak doğru olmaktadır."

Doğal dilde kullandığımız birçok cümlede “az”, “çok”, “orta” gibi kalitatif niceleyiciler kullanıyoruz. Bu tür cümleleri bulanık mantığın gösterimi ile ifadelendirmek daha kolay olmaktadır. Bulanık mantıkta “Ahmet yaşlıdır” ve “Bugün hava sıcaktır” cümlelerindeki “yaşlı” ve “sıcak” ifadelerine iki değerli mantıktaki gibi “doğru” veya” yanlış” yerine 0 ile 1 arasında değer verilebilmektedir.

Bulanık mantığın formel tanımları

X, elemanları x’ler olan bir nesneler kümesi olsun, yani X = ( x ). X’in içinde bir A bulanık kümesi bir üyelik fonksiyonu mA(x) ile karakterize edilir. Bu fonksiyon X içindeki her nesneyi, 0 ile 1 arasındaki bir reel sayıya [0,1] tekabül ettirir. Yukarıdaki örnekte A, yaşlı insanlar kümesi olabilir. Ahmet de X insanlar genel kümesinin bir üyesi olarak yaşlı insanlardan biri olabilir, ki A’daki üyelik derecesine göre üyelik değeri [0,1] reel sayılar aralığında yer alır.

mA(x) değeri 1’e yaklaştığında x’in A içindeki “üyelik derecesi” artar. Bütün x’ler için mA(x) = 0 ise, A boş bir küme olur ve bütün x’ler için mA(x) = mB(x) olduğunda da A=B olur. Bulanık kümelerle ilgili tarifler de şöyledir:

m(karşıt A) = 1 – mA.

Eğer X’in bütün x’leri için mC(x) = MAX[mA(x), mB(x)] ise, C, A ve B’nin birleşimidir.

Eğer X’in bütün x’leri için mC(x) = MIN[mA(x), mB(x)] ise, C, A ve B’nin arakesitidir.